【図解】ニューラルネットワークの活性化関数とは?【連載③】

どうもあつかんです。
今回はニューラルネットワークに使用される活性化関数について説明していこうと思います。
ゼロから作るDeep Learningという本を参考にさせていただいております。
また、このブログは連載形式ですので下の記事を読んでから読むことおすすめします。
活性化関数とは?
活性化関数については
【初心者向け】ニューラルネットワークとは?【連載②】 - IT-LIFEブログ
で簡単な説明がしてありますが、ここでも少し説明しようと思います。
活性化関数とは入力信号の総和をどのように活性化(発火)させるを決定する役割があります。
活性化関数にも複数の種類があり、ステップ関数、シグモイド関数、ReLU関数というものがあります。
過去記事からわかるようにパーセプトロンでは活性化関数としてステップ関数が使われていましたね。
ステップ関数とは下図のように閾値を超えていたら1を出力、閾値を超えていなかったら0を出力するような関数でした。
ここで質問です。
パーセプトロンをニューラルネットワークの世界に拡張させるためにはどうしたらよいでしょうか?
答えは、パーセプトロンで使われている活性化関数を別の関数に置き換えることで、ニューラルネットワークの世界へ進むことができます。
では、ニューラルネットワークで使われている活性化関数を見ていきましょう。
様々な活性化関数
シグモイド関数
シグモイド関数はニューラルネットワークでよく使われる関数の一つです。
式は以下のようにあらわされます。

exp(-x)はeの-x乗という意味です。eはネイピア数で2.7182.......の実数です。
グラフは下図のような形になります。
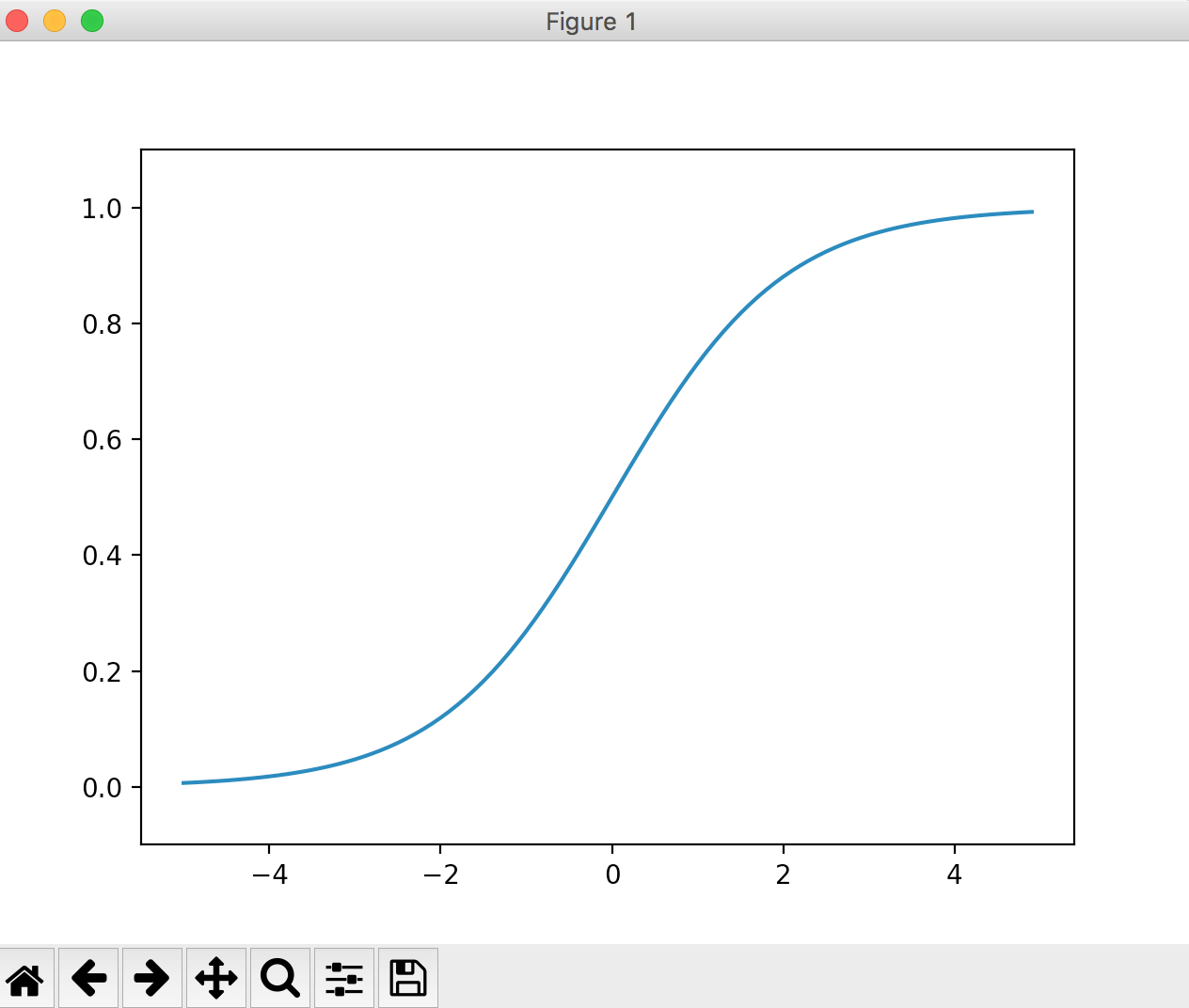
ニューラルネットワークとパーセプトロンの主な違いは、この活性化関数だけです。
パーセプトロンはステップ関数、ニューラルネットワークはシグモイド関数など。
これだけなのです。
それではステップ関数とシグモイド関数を比較するためにグラフを重ねてみます。

この図をみて気づく点は、グラフの”滑らかさ”の違いだと思います。
シグモイド関数は入力に対して連続的(滑らかに)に変化していますが、ステップ関数は0を境にして急激に値が変化しています。
この違い、つまりシグモイド関数の滑らかさがニューラルネットワークの学習において重要な意味をもっています。
その理由は今後の記事で紹介していきます。
また、ステップ関数は1か0の値のみしか出力しませんが、シグモイド関数は0から1の間の実数(0.37469や0.98893など)を返します。
つまり、デジタル的な変化でなく、アナログ的な変化を含ませたわけです。
人間の脳はアナログの情報でやり取りしていますので、それに近づいたわけですね。
ステップ関数とシグモイド関数の共通点として、両者とも入力が小さいときほど小さい値を出力し、入力が大きい値ほど大きい値を出力しています。
つまり、重要な信号であれば大きな値を出力し、重要でない信号であれば小さな値を出力します。
また、出力の値は0から1の間のみだということもわかります。
ReLU関数
これまでに、活性化関数としてステップ関数とシグモイド関数を紹介しました。
シグモイド関数はニューラルネットワークの歴史において古くから使用されています。
しかし、近年ではReLU (Rectified Linear Unit) 関数という活性化関数が主流となっているようです。
この関数は0を超えていれば入力の値をそのまま出力し、0を超えていない場合は0を出力するといった単純な関数です。
図で表すとこんな感じ。
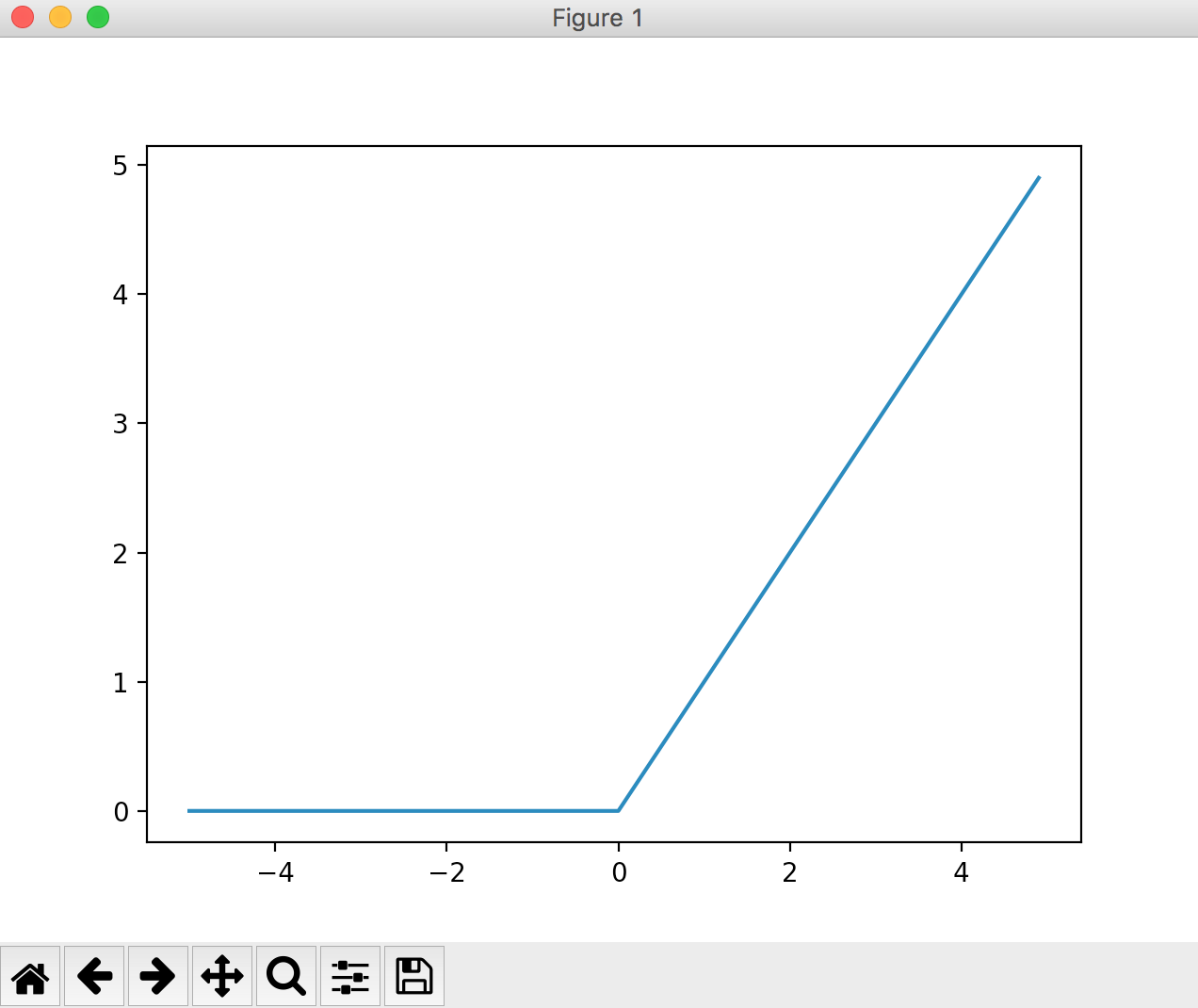
式で表すとこんな感じ。

とても簡単な式ですね。
閾値以下の入力は0(重要でない)、閾値以上の入力は入力の値をそのまま出力、つまり重要度に比例した値を出力するといった機構ですね。
以上で活性化関数の説明は終わりです。
まとめ
今回は活性化関数について紹介していきました。
パーセプトロンの活性化関数はステップ関数であり、その活性化関数をステップ関数以外の関数に置き換えることにより、パーセプトロンをニューラルネットワークの世界に持っていけるということが分かりました。
ステップ関数以外の関数とは、シグモイド関数、ReLU関数などでした。
ではなぜ、シグモイド関数や、ReLU関数がニューラルネットワークに使用されるのか?
それは二つの関数にはステップ関数にはない”滑らかさ”があるからでした。
その”滑らかさ”が、ニューラルネットワークの得とする”学習”にとって非常に大切な意味を持ちます。
なぜなのか?
それについては今後のブログで書いていきますのでご安心を♪
ではでは。
続きの連載④はこちらです。
